НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ЯДЕРНЫЙ УНИВЕРСИТЕТ
МИФИ
Факультет «Автоматики и Электроники»
Кафедра №27
Дисциплина: Компьютерный практикум-16
«Функциональные узлы цифровой автоматики»
Подготовил: студент группы А04-11 Янгляев Р.Р.
Преподаватель: доцент Лапшинский В. А.
Москва 2016
(Версия 3.0 воскресенье, 31 мая 2016 г.)
НИК - Yanglyaev
Подпись на форуме - Пишите громче, я вас не слышу.
Аннотация
Конспект посвящён введению в цифровую электронику. Даны необходимые базисные сведения об алгебре логике, комбинационных устройствах (дешифраторах, шифраторах и т.д), последовательностных устройствах (триггерах и регистрах, счетчиках).
В конспекте: 24 страниц, 12 иллюстраций, 1 таблица.
Ключевые слова: Семотехника, логическая схема, И, ИЛИ, НЕ, И-НЕ, ИЛИ-НЕ.
Глоссарий
- ТТЛ - транзисторно-транзисторная логика
- БИС – большая интегральная схема
- СДНФ - Совершенная дизъюнктивная нормальная форма
- ПЛМ - программируемых логических матриц
- ПЗУ – постоянное запоминающее устройство
- ЭСЛ - Эмиттерно-связанная логика
Оглавление
Предисловие
Глава 1. ВВЕДЕНИЕ В АЛГЕБРУ ЛОГИКИ
1.1. Функции НЕ, И, ИЛИ. Булевский бази
1.2. Функции И-НЕ и ИЛИ-НЕ
Глава 2. КОДИРУЮЩИЕ УСТРОЙСТВА
2.1. Дешифраторы
2.2. Мультиплексоры
2.3. Шифраторы
2.4. Преобразователи произвольных кодов
2.5. Программируемые логические матрицы
Заключение
Список использованных источников
Предисловие
В процессе разработки функциональных сем цифровых устройств отчетливо выделяются два характерных этапа. На первом этапе, который можно назвать структурным проектированием, заданный неформально алгоритм разработчик представляет в виде последовательности некоторых операторов, таких, как хранение чисел, и сравнение или сложение, коммутация каналов передачи. При этом он старается использовать ограниченный набор по возможности общепринятых операторов. После этого можно приступать ко второму этапу – построению самих логических схем, реализующих требуемые операторы. Схемы, реализующие общепринятые операторы, называют функциональными узлами или просто узлами.
Глава 1. ВВЕДЕНИЕ В АЛГЕБРУ ЛОГИКИ
Алгебра логики – это формальный аппарат описания логической стороны процессов в цифровых устройствах. Алгебра логики имеет дело с логическими переменными, которые могут принимать только два значения, называемые ИСТИНА и ЛОЖЬ, а также их называют TRUE и FOLS, ДА и НЕТ, но наиболее распространено обозначение 1 и 0. При этом 1 и 0 нельзя трактовать как числа, над ними нельзя производить арифметические действия. Это просто коротая запись (для удобства) обозначающая понятия ДА и НЕТ, это как номер трамвая – краткая форма наименования его маршрута.
Логические переменные хорошо описывают состояния таких объектов, как реле, тумблеры, кнопки и т.п., соответственно объектов, которые могут находится в двух четко различимых состояниях: вкл. – выкл.
1.1. Функции НЕ, И, ИЛИ. Булевский базис
Набор трех логических функций: НЕ, И, ИЛИ называют булевским или булевым базисом в честь английского математика конца XIX века Джорджа Буля, исследовавшего эти функции. Алгебру, в которой различные логические функции выражаются через эти три функции, называют булевой алгеброй.
Функция НЕ – это функция одного аргумента (отрицание, инвер-сия). Функция обычно обозначается чертой над аргументом:
Y=ā,
где Y – логическая функция, а – аргумент. Встречаются и другие обозначения: Y=НЕа или Y= ┐а. Функция отрицания равна 1, когда ее аргумент равен 0, и наоборот:
ПОГАШЕН=НЕ(ГОРИТ)
Если утверждение ГОРИТ истинно, то утверждение ПОГАШЕН ложно, и наоборот. Важно подчеркнуть что, Отрицание отрицания аргу-мента равно самому аргументу: НЕ(НЕ ГОРИТ)=ГОРИТ. Инвертор на функциональных схемах изображается, как показано на (рис 1).
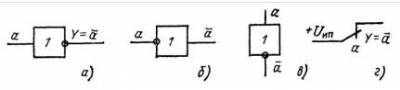
Рис. 1. Инвертор
Функция И – это функция двух или большего числа аргументов (конъюнкция, логическое умножение, совпадение, AND). Обозначение:
Y=a&b; Y=a▪b; Y=ab.
Функция И равна 1 тогда и только тогда, когда все ее аргументы равны 1. Союз “и” естественного языка, как правило, выражает именно это отношение, например: ЛИФТ ПОЙДЕТ, если ДВЕРЬ ЗАКРЫТА И КНОПКА НАЖАТА, или в аналитической записи: L=dk, где L – выходной сигнал на двигатель лифта; d – входной сигнал закрытия двери; k – выходной сигнал нажатой кнопки. Условное изображение элемента И показано на (рис. 2).
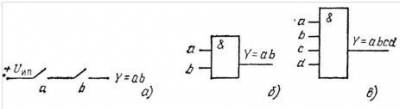
Рис. 2. Конъюнктор
Функция ИЛИ – это функция двух или большего числа аргу-ментов. Функция ИЛИ равна 1, если хотя бы один из ее аргументов равен 1. Обозначение:
Y=a˅b.
Используемые иногда значения + и название функции “логическое сложение” неудачны, поскольку в сложных случаях дизъюнкция будет смешиваться с другими операциями. В русском языке функция дизъюнкции выражается союзом ИЛИ, во фразу типа: Мы попадем на тот берег, если речка мелкая или мост цел. Формальная запись ТБ=РМ˅МЦ. Условное изображение на схеме элемента, реализующего функцию ИЛИ – показано на (рис. 3).
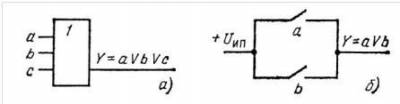
Рис. 3. Дизъюнктор
1.2. Функции И-НЕ и ИЛИ-НЕ
Функция И-НЕ - это функция двух и более аргументов (другие названия: штрих Шеффера, функция Шеффера, NAND). Значения функции представлены в таблице 1. Легко видеть, что это инверсия функции И, т. е. отрицание конъюнкции. Любой 0 на входе дает 1 на выходе, все единицы на входе дают 0 на выходе. Специального символа для обозначения И-НЕ не применяют, используя комбинацию символов И и HE.
Способность функции И-НЕ выражать только через само себя все функции булева базиса доказывает, что эта функция обладает логическое полнотой. С помощью одной лишь функции И-НЕ можно построить любую сколь угодно сложную логическую функцию. Вторым ценным свойством функции И-НЕ оказалось то, что именно ее удалось эффективно реализовать средствами самой массовой интегральной технологии – ТТЛ. Поэтому уже четверть века функция И-НЕ наиболее распространена в цифровой автоматике. Выпускается И-НЕ в виде отдельных микросхем, на ее основе создано множество схем средней интеграции, И-НЕ широко используется в семах с большой степенью интеграции (БИС). Аналога в русском языке эта схема не имеет, поэтому мышление в базисе И-НЕ непривычно и требует тренировки[1].
Функция ИЛИ-НЕ – это функция двух и более аргументов (другие названия: функция Вебба, стрелка Пирса, NOR). Значение функции представлены в табл.1. Данная функция является инверсией функции ИЛИ. Русский язык немного умеет оперировать с этой функцией, называя ее “ни - ни”. Так, фраза Y есть ни рыба, ни мясо утверждает, что названный объект не принадлежит ни к одному из этих классов. Функция ИЛИ-НЕ, как и функция И-НЕ, обладает полнотой и тоже удобна для интегрального исполнения, особенно по технологии КМДП и ЭСЛ. Функция ИЛИ-НЕ – вторая по распространенности после И-НЕ функции в цифровой технике.
Глава 2. КОДИРУЮЩИЕ УСТРОЙСТВА
2.1. Дешийфраторы
Дешифратором или декодером (decoder), чаще всею называют кодирующее устройство, преобразующее двоичный код в унарный. Из всех m выходов дешифратора активный уровень имеется только на одном, а именно на том, номер которого равен поданному на вход двоичному числу. На всех остальных выходах дешифратора уровни напряжения неактивные.
Декодер используют, когда нужно обращаться к различным цифровым устройствам, и при этом номе устройства – его адрес – представлен двоичным кодом. Воды декодера часто нумеруются не порядковыми номерами, а в соответствии с весами двоичных разрядов, т.е. не 1, 2, 3, …, а 1, 2, 4, 8, 16, …. Число входов и выходов декодера указывают таким образом: декодер 3-8 (читается как три в восемь); 4-16; 4-10 (это не полный декодер). Дешифраторы часто имеют разрешающий вход Е. При Е=1 дешифратор, работает как обычно, при Е=0 на всех выходах устанавливаются неактивные уровни независимо поступившего кода адреса. Вход Е часто выполняют инверсным. Дешифратор, имеющий разрешающий вход, иногда называют декодер-демультиплексор и на условном обозначении вместо символа DC используют символ DX.
2.2. Мультиплексоры
Мультиплексоры (multiplexor) – это функциональный узел, осуществляющий подключение (коммутацию) одного из нескольких входов данных к выходу. Номер выбранного входа соответствует коду, поданному на адресные входы мультиплексора. Вход Е – разрешающий: при Е=1 мультиплексор работает как обычно, при Е=0 выход узла находится неактивном состоянии, мультиплексор запер.
 Мультиплексор можно использовать в качестве универсального логического элемента для реализации любой функции от числа аргументов, равного числу адресных входов мультиплексора. Не удивительно, что способ реализации функции трех или четырех аргументов с помощью микросхемы мультиплексора весьма популярен у разработчиков. Следует помнить, что этот способ может дат экономию лишь при использовании микросхем. При разработке схем для кристаллов матричных и других БИС объем оборудования определяется числом базовых логических элементов, поэтому такой способ будет крайне расточительным.
2.3. Шифраторы
Шифратор, или кодер (encoder), выполняет функцию, обратную дешифратору. Классический шифратор имеет m входов и n выходов, и при по-даче сигнала на один из входов (обязательно на один, и не более) на выходе узла появляется двоичный код номера возбужденного выхода.
Совместно с шифратором, а состав кодирующих узлов может входить схема выделения старшей единицы. Эта схема преобразует m-разрядное слово следующим образом: все старшие нули и самая старшая единица входного кода пропускаются на выход без изменения; все разряды, более младшие, чем старшая единица, заменяются нулями.
2.4. Преобразователи произвольных кодов
Если закон работы преобразователя не описывается каким-либо достаточно понятным правилом, как, например, работа декодера или шифратора, то единственной практически приемлемой формой задания преобразователя становится таблица. Поскольку таблица воплощает в себе идею полного перебора вариантов, она способна задавать абсолютно любой закон.
При подходе к построению кодового преобразователя он трактуется как пара декодер – кодер. Схема того же преобразователя, построенного по этому способу, показана на (рис. 4б). Число входов дешифратора равно числу входов преобразователя, число выходов шифратора – числу выходов преобразователя. Часть выходов декодера и входов кодера может не использоваться. Если нескольким входным комбинациям соответствует одна и та же выходная, то соответствующие выходы декодера объединяют на элементе ИЛИ и выход последнего подают на нужный вход кодера.
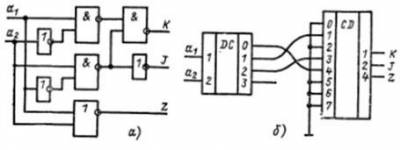
Рис. . Кодовый преобразователь
На (рис. 4а) показано возможная реализация кодового преобразователя, заданного в базисе И-НЕ, ИЛИ-НЕ, учитывающая связность выражений. В более сложных многовыходных схемах экономия от учета связности обычно оказывается существенно большей, чем в рассмотренном очень простом примере, однако каких-либо алгоритмов эффективного целенаправленного выявления общих частей, к сожалению, не существует. Как и синтез оптимальной одновыходной схемы, это поисковая задача, только обычно еще более сложная из-за большого числа возможны вариантов.
2.5. Программируемые логические матрицы
Исключительная простота синтеза произвольных кодовых преобразователей по принципу декодер – кодер обусловила выпуск микросхем средней и даже большой интеграции, специально предназначенных для реализации кодовых преобразователей. Это микросхемы программируемых логических матриц – ПЛМ.
Элементы ИЛИ в ПЛМ, так же, как и элементы И, имеют на входах выжигаемые перемычки, с помощью которых они подключены ко всем вертикальным шинам, после выжигания на программаторе ненужных перемычек у элементов ИЛИ также остаются лишь те связи вертикалями, которые необходимы потребителю. Техническая реализация элементов ИЛИ такова, что после выжигания перемычек на входах И обеспечиваются уровни логического нуля.
Заключение
Если вы внимательно изучили все предложенную информацию значит, вы получили начальное представление о мире цифровой автоматики. К сожалению, не слишком большой объем конспекта не позволил в полной мере раскрыть все приемы работы и подробно описать многочисленные процессы в цифровой автоматике. Попробуйте самостоятельно изучить компоненты, не вошедшие в конспект. Не бойтесь экспериментов. Удачи.
Список использованых источников
- Потемкин И. С. Функциональные узлы цифровой автоматики. – М.:энергоатомиздат, 1988. – 320 с.: ил.
- Измерение параметров цифровых интегральных микросхем/Д Ю. Эйдукас, Б. В. Орлов, Л. М. попель и др. ; Под ред. Д. Ю. Эйдукаса, Б. В. Орлова. М.: Радио и связь, 1982.
- Зельдин Е. А. Триггеры. М.: Энергоатомиздат, 1983.
| 
