| Статистика |

Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
|
Математическое мышление
Научно-исследовательский ядерный университет
Московский инженерно-физический институт
Факультет «Автоматики и электроники»
Кафедра «Микро- и наноэлектроники»

Курс «Компьютерный практикум»
Математическое мышление
Преподаватель: доцент В.А. Лапшинский
Подготовил студент А4-11
Ломака А.С.
Москва 2014 (31.03.2014, v. 3)

LMK
Аннотация
В сборник включены произведения выдающегося математика современности Германа Вейля (1885-1955), посвященные теоретико-познавательным проблемам математики, ее взаимодействиям с науками о природе, роли в исследовании внешнего мира и творчеству замечательных ученых Д. Гильберта, Ф. Клейна, Э. Нетер, А. Пуанкаре, Э. Картана и В. Паули. Для математиков, физиков, историков науки и философов.
Ключевые слова: математическое мышление, Множество и функция.
Глоссарий
1. Математическое мышление-это наука о формах, методах и законах интеллектуальной познавательной деятельности, формализуемых с помощью логического языка. Поскольку это знание получено разумом, логика также определяется как наука о формах и законах правильного мышления.
2. МНОЖЕСТВО это-одно из основных понятий современной математики, “произвольная совокупность определенных и различимых объектов, объединенных мысленно в единое целое”
3. Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемого областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
Введение
Скучной, конечно же, математика быть не может.
Она может быть только занимательной!
Этот конспект посвящен книжке-задачнику [1] по наиболее острым вопросам издательской работы. Занимательная редактология придумана для того, чтобы секреты редактуры, дизайна и верстки для школьный издателей перестали быть великой и страшной тайной.
Математическое мышление
Исследования многих отечественных и зарубежных психологов показывают, что без целенаправленного развития математического мышления, являющегося одним из важнейших компонентов процесса познавательной деятельности, невозможно достичь эффективных результатов и обучении, систематизации знаний, умений и навыков. К сожалению, единого мнения по вопросу определения понятия математического мышления в психолого-педагогической и методической литературе нет. При его характеристике возникают сложные вопросы о взаимосвязи этого понятия с понятиями мышление вообще и конкретные виды мышления. Одни исследователи считают, что математического мышления как такового, обладающего своими специфическими формами мыслительных действий, нет; своеобразие такого мышления связано, по их мнению, лишь с характером собственно математического материала. Другими словами, представители первого подхода отрицают специфику математического мышления.
Множество
МНОЖЕСТВО [set] — одно из основных понятий современной математики, “произвольная совокупность определенных и различимых объектов, объединенных мысленно в единое целое”. (Так определял М. основатель теории множеств, известный немецкий математик Георг Кантор. Правда, уже в начале XX в. стало ясно, что определение Кантора нельзя считать достаточно строгим, так как оно приводит к различным логическим противоречиям. Широко распространено убеждение, что М. — понятие, поясняемое только на примерах. Такая странная для математики ситуация объясняется отчасти тем, что все попытки определить термин “М.” приводят, по существу, к замене его другими, столь же неопределенными понятиями.)
Примеры множеств: М. действительных чисел, М. лошадей в табуне, М. планов, М. функций, М. переменных задачи.

Рис. 1 Множество
Все М., кроме пустого М., состоят из элементов. Напр., каждое действительное число есть один из элементов М. действительных чисел. То, что эле-мент a принадлежит множеству A, обозначают с помощью специального знака a ∈ A. Это читается так: “a принадлежит множеству А в качестве элемента”.
М. можно задать прямым перечислением элементов. Пусть А состоит из эле-ментов a1, a2, a3. Это записывается так: A = {a1, a2, a3}. Если непосредственное перечисление элементов М. невозможно (напр., когда М. A состоит из бесконечного числа элементов), его определяют характеристическим высказыванием, т. е. высказыванием, истинным только для элементов данного М. В та-ком случае употребляется запись типа:
A = {x|P(x) = И}, которая читается так: “Множество A есть множество, состоящее из элементов x таких, чтоP(x) — истинно”. Множество М всех планов x, удовлетворяющих условию, что они лучше (больше), чем план x0, может быть задано с помощью высказывания: М {x|(x>x0) = И} или сокращенно M = {x|(x>x0}.
Коротко остановимся на определениях и свойствах действий над множествами.
Прежде всего можно рассмотреть два М. — A и B, обладающих следующим свойством: все элементы М. A принадлежат и М. B. М. A есть, таким об-разом, подмножество B. Это обозначается так: A ⊂ B. Предположим теперь, что даны произвольные М. A и B. Тогда из элементов этих М. можно сконструировать несколько других.
Во-первых, М. элементов, принадлежащих либо A, либо B; такая операция над М. обозначается A ∪ B и называется объединением; ясно, напр., что если A ⊂ B, то A ∪ B = B; кроме того, A ∪ B = B ∪ A (это свойство называется коммутативностью); (A ∪  ∪ C = A ∪(B ∪ C) — это свойство ассоциативности(возможность произвольного разбиения на группы). ∪ C = A ∪(B ∪ C) — это свойство ассоциативности(возможность произвольного разбиения на группы).
Во-вторых, можно рассмотреть также М. элементов, принадлежащих и A, и B одновременно; такая операция называется пересечением и обозначается ∩. Предположим, что A ⊂ B, тогда A ∩ B = A. Для того, чтобы пересечение двух М. имело смысл, даже если у них нет общих элементов, вводится понятие пустого М., т. е. М. без элементов. Его обозначают ∅. Легко увидеть, что A ∪ ∅ = A; A ∩ ∅ = ∅.
Так же, как и объединение, операция ∩ — ассоциативная и коммутативная.
Объединение множеств называют иногда их суммой, а их пересечение — произведением.
В-третьих, можно выделить также подмножество элементов М. A, не принадлежащих B. Это действие называется дополнением B до A или разностью A\B. Так же, как и в случае обычной разности, это действие некоммутативно.
Функция
Наиболее строгим определением функции является теоретик множественное определение (на основе понятия бинарного отношения). Часто вместо определения функции даётся её интуитивное описание; то есть понятие функции переводится на обычный язык, используя слова «закон», «правило» или «соответствие».
Интуитивное описание
Функция (отображение, операция, оператор) — это закон или правило, согласно которому каждому элементу из множества ставится в соответствие единственный элемент из множества При этом говорят, что функция задана на множестве, или что отображает.
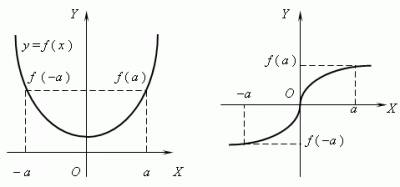
Рис. 2 Функция
Если элементу сопоставлен элемент , то говорят, что элемент находится в функциональной зависимости от элемента . При этом переменная называется аргументом функции или независимой переменной, множество называется областью задания или областью определения функции, а элемент , соответствующий конкретному элементу — частным значением функции в точке . Множество всех возможных частных значений функции называется её областью значений или областью изменения.
Теоретико-множественное определение[
Функция есть множество упорядоченных пар ), которое удовлетворяет следующему условию: для любого[3] существует единственный элемент такой, что .
Таким образом, функция — это упорядоченная тройка (или кортеж) объектов , где множество называется областью определения; множество называется областью значений; множество упорядоченных пар или, что то же самое, график функции.
Заключение
Надеюсь, данный конспект поможет студентам кафедры «МНЭ» МИ-ФИ (и, возможно, участникам будущей олимпиады «Наноэлектроника») начать развитие математического мышления. И применить эту науку на практике. Например, при решении задач как в домашних условиях так и на олимпиаде. После прочтения этого конспекта, читатель должен понять основы математического мышления.
Список литературы
1. Вейль Г. Математическое мышление: Пер. с англ. и нем. / Под ред. Б.В.Бирюкова и А.Н.Паршина. — М.: Наука. Гл. ред. физ.-мат. лит, 1989. - 400 с. - ISBN 5-02-013910-6.
2. В сборник включены произведения выдающегося математика современности Германа Вейля (1885-1955), посвященные теоретико-познавательным проблемам математики, ее взаимодействиям с наука-ми о природе, роли в исследовании внешнего мира и творчеству замечательных ученых Д. Гильберта, Ф. Клейна, Э. Нётер, А. Пуанкаре, Э. Картана и В. Паули.
3. http://www.elitarium.ru/2011/10/24/zagolovok_vsemu_golova.html-
Для математиков, физиков, историков науки и философов
– множество.
4. Лапшинский В.А. Методические рекомендации по оформлению конспекта. – М.: МИФИ, 2013. – 10 с. |
| Категория: Конспекты (курсы КП и ПК) | Добавил: LMK (07.08.2014)
|
| Просмотров: 582
| Рейтинг: 0.0/0 |
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
|