| Статистика |
Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
|
Стойкость биполярных приборов
Оглавление
Введение 3
Методики прогнозирования эффекта низкой интенсивности 4
Конверсионная модель эффекта низкой интенсивности 6
Использование конверсионной модели для описания экспериментальных данных 8
Аппроксимация экспериментальных данных степенной функцией 11
Заключение 15
Литература 16
Введение
Воздействие на изделия электронной техники ионизирующего излучения низкой интенсивности характерно для аппаратуры космического применения, где мощность дозы составляет 〖10〗^(-2)-〖10〗^(-5) рад/с. Это существенно превышает мощность дозы, обычно используемую при радиационных испытаниях (50-300 рад/c).
Низкочастотное облучение биполярных микроэлектронных структур имеет способность: при снижении интенсивности ионизирующего излучения происходит усиление деградации коэффициента усиления биполярных транзисторов при наборе одинаковой поглощенной дозы. Этот эффект носит название эффекта низкой интенсивности в биполярных приборах (ELDRS).
Методики прогнозирования эффекта низкой интенсивности
Облучение испытуемых приборов при интенсивности 10 мрад/c дополнительной дозой с коэффициентом облучения 1.5.
Использование облучения с интенсивностью 50-300 рад/с при повышенной температуре 1000С.
Указанные методики позволяют получить так называемую, консервативную оценку предельно допустимой дозы, то есть заниженное значение допустимой дозы, но без указания, даже приблизительного, величины запаса по дозе. Но существует расчетная методика оценки стойкости полупроводниковых приборов и микросхем к воздействию низкоинтенсивного излучения космического пространства. Преимуществом расчетной методики является учет зависимости деградации параметров биполярных структур от величины интенсивности ионизирующего излучения или мощности дозы. Полагается, что в диапазоне 0,05-100 Р/с зависимость предельной дозы отказов от интенсивности описывается степенной функцией:
D_отк=A(γ)^m
Где D_отк- доза отказов; А - подгоночный параметр; γ – интенсивность излучения, измеряемая в Р/c; m – показатель степенной функции. В табл. 1 приведены экспериментальные значения параметров этой аппроксимирующей зависимости для некоторых отечественных микросхем.
Таблица 1
Параметры аппроксимации соотношения (1) для биполярных цифровых интегральных схем
Тип ИС Критерий отказа A m
134ЛБ1 I_OL≤12 мА 5.5∙〖10〗^4 0.22
1505ЛБ1 I_OL≤20 мА 1.8∙〖10〗^5 0.21
1533ЛБ1 ФК 3.0∙〖10〗^6 0.16
530ИР18 U_OL≤0.5 В 2.0∙〖10〗^7 0.26
541РУ1 ФК 1.4∙〖10〗^5 0.17
1615РУ11 ФК 9.5∙〖10〗^5 0.23
ФК – функциональный контроль
К сожалению, в [6] не приводятся значения параметров аппроксимации предложенного вида, что совершенно необходимо для результатов, на основании которых РД 319.03.37-2000 расширяет применение показателя m=0,26 на все типы дискретных микросхем и биполярных транзисторов n-p-n типа.
Несмотря на то, что отечественные отраслевые стандарты учитывают зависимость деградации приборов от интенсивности ионизирующего излучения, диапазон интенсивности 0.05 – 100 Р/с, в котором справедливо соотношение (1), выбран произвольно. Полностью отсутствует информация об изменении предельной зоны отказа для этого диапазона. Использование значения показателя m=0,26 для всех биполярных приборов нельзя считать обоснованным.
Для устранения недостатков рассматриваемых методик в МИФИ разрабатывается конверсионная модель низкой интенсивности. Эта модель позволяет в простой аналитической форме описать деградацию коэффициента усиления во всем диапазоне интенсивностей.
Конверсионная модель эффекта низкой интенсивности
Определение «конверсионная модель» основывается на предположении, что эффект низкой интенсивности связан с особенностями накопления радиационно-индуцированных поверхностных состояний. Полагается, что генерация поверхностных состояний происходит при нейтрализации радиационно-индуцированного положительного заряда электронами из полупроводника, т.е. за счет конверсии отжигаемого положительного заряда в поверхностные состояния. Определение «конверсионная модель» связано с принятой за основу конверсионной природой накопления поверхностных состояний.
Предполагается, что существуют мелкие и глубокие ловушки положительного заряда. За короткое время облучения высокой интенсивностью происходит конверсия только мелких ловушек. При длительном облучении низкой интенсивностью дополнительно конвертируются глубокие ловушки, что приводит к деградации тока базы. В математической форме зависимость деградации тока базы от интенсивности ионизирующего излучения описывается выражением:
ΔI_Б=(K_Г+K_М )D+γK_Г τ_Г (e^(-γ)-1)
Где ΔI_Б – приращение тока базы, K_Г - коэффициент характеризующий приращение тока базы за счет конверсии глубоких ловушек и равный приращению тока базы на единицу поглощенной дозы при низкой интенсивности; K_М – коэффициент, характеризующий приращение тока базы за счет конверсии мелких ловушек и равный приращению тока базы на единицу поглощенной дозы при высокой интенсивности; D – суммарная поглощающая доза; γ – интенсивность ионизирующего излучения, τ_Г - время конверсии глубоких ловушек.
Зависимость имеет инверсную S-образную характеристику (рис. 1). Приращение тока базы при высоких интенсивностях (малых временах облучения) определяется накоплением и конверсией мелких ловушек, успевающих за короткое время облучения конвертироваться в поверхностные состояния. Величина приращения тока базы при этом равна K_М D.
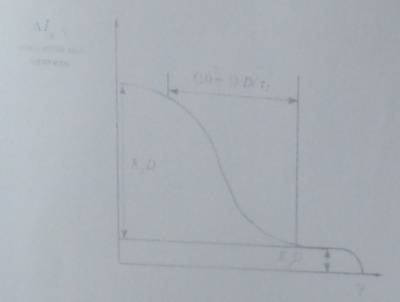
Рис. 1. Зависимость приращения тока базы от интенсивности при постоянной накопленной дозе
При уменьшении интенсивности или с увеличением времени облучения плотность поверхностных состояний увеличивается за счет конверсии глубоких ловушек, характерное время конверсии которых значительно больше, чем у мелких ловушек. Переходная область по времени составляет 3-5 τ, где τ - постоянная времени конверсии глубоких ловушек. Диапазон интенсивности, где с ее уменьшением наблюдается рост приращения тока базы, составляет 10¬^(-3) D.
При очень малых интенсивностях или очень больших временах облучения практически все глубокие ловушки успевают конвертироваться, поэтому приращение тока снова достигает некоторого постоянного значения. Приращение тока базы при этом увеличивается относительно высокой интенсивности на величину K_г D, где Kг - коэффициент характеризующий приращение тока базы за счет конверсии глубоких ловушек.
Конверсионная модель имеет три подстроенных коэффициента. Экстраполяция этих коэффициентов позволяет рассчитать полную инверсную S-образную характеристику и прогнозировать деградацию тока базы для любой заданной интенсивности и суммарной накопленной дозе облучения
Использование конверсионной модели для описания экспериментальных данных
На рис. 2-5 показаны экспериментальные и расчетные и расчетные зависимости приращения тока базы от интенсивности облучения. Расчет хорошо согласуется с экспериментом при значениях подстрочных коэффициентов, сведенных в таблице 2.
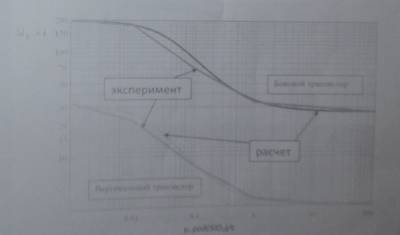
Рис. 2. Зависимость приращения тока базы вертикального и бокового p-n-p транзистора от интенсивности облучения при дозе 30 крад(SiO2)
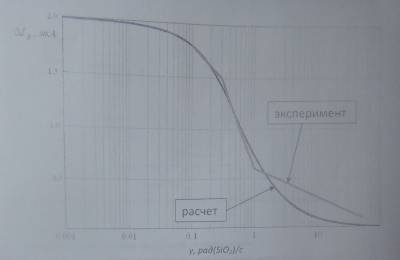
Рис. 3. Зависимость деградации входного тока прибора LM111 от интенсивности облучения при дозе 300 крад(SiO2)
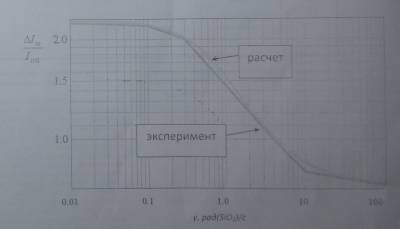
Рис. 4. Зависимость относительной деградации входного тока прибора 2N2907 от интенсивности облучения при дозе 30 крад(SiO2)
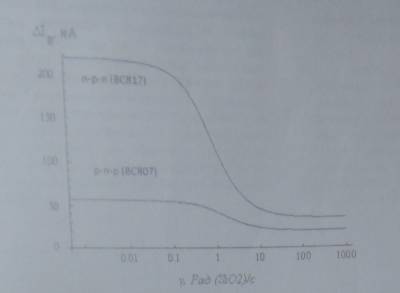
Рис. 5. Зависимость приращения тока базы транзисторов n-p-n (BC817) и p-n-p (BC807) от интенсивности облучения при дозе 30 крад(SiO2)
Таблица 2
Экспериментальное значение подстрочных коэффициентов
K, нА/рад(SiO2) Kг, нА/рад(SiO2) τг, с Доза, крад(SiO2) Прибор Литература
1,4∙〖10〗^(-3) 8,7∙〖10〗^(-6) 2,2∙〖10〗^5 20 Боковой p-n-p [8]
1,6∙〖10〗^(-4) 1,5∙〖10〗^(-5) 5,0∙〖10〗^5 20 Вертикальный p-n-p [8]
3,3∙〖10〗^(-4) 6,3∙〖10〗^(-5) 3,0∙〖10〗^5 300 LM111 [9]
2,2∙〖10〗^(-5) 3,9∙〖10〗^(-4) 1,0∙〖10〗^4 30 2N2907 [10]
1,2∙〖10〗^(-3) 6,1∙〖10〗^(-3) 2,1∙〖10〗^4 30 n-p-n (BC817) [11]
6,8∙〖10〗^(-4) 1,2∙〖10〗^(-3) 1,1∙〖10〗^4 30 p-n-p (BC 807) [11]
Аппроксимация экспериментальных данных степенной функцией
Использование аналитической функции (2) позволяет определить показатель степенной функции m в выражении (1), при котором степенная функция хорошо аппроксимирует экспериментальные данные. На рис. : в качестве примера показана зависимость ln〖D_отк 〗 от lnγ, которая хорошо аппроксимирует экспериментальную зависимость приведенную на рис. 3. Подобное представление может быть построено для всех рассматриваемых выше приборов и выбрано потому, что степенная функция (1) в логарифмических координатах ln〖D_отк 〗 от lnγ соответствует линейной функции с наклоном показателя степени m. Используя аппроксимации реальных экспериментальных данных на рис. 2-5, можно определить значение коэффициента m, при котором степенная функция хорошо описывает данные эксперимента для всех рассматриваемых приборов.
Были исследованы два типа аппроксимаций: в широком диапазоне интенсивностей и локально для каждой интенсивности. В первом случае получилось интегральное значение коэффициента m. Во втором – дифференциальное значение показателя степени для каждой интенсивности.
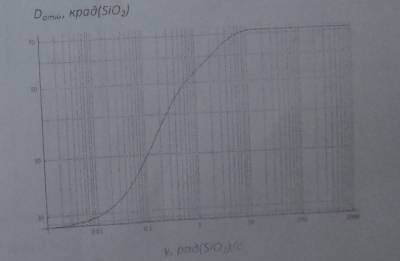
Рис. 6. Зависимость дозы отказа D_отк от ионизирующего излучения γ в логарифмических координатах.
Для первого случая выбирался диапазон интенсивностей, примерно соответствующий началу и концу нелинейного изменения дозы отказов от интенсивности на рис. 6. Наклон прямой линии между этими интенсивностями соответствовал интегральному значению коэффициента m. Граничные интенсивности выбирались из условия изменения предельной дозы отказов на 3% относительно максимального и минимального значения предельных доз. Подобные построения проведены для всех четырех исследуемых приборов и вычислены соответствующие значения показателя степени m.
Таблица 3
Интегральные значения показателя степени m
Прибор Интервал интенсивности, рад(SiO2)/с Показатель степени m Литература
Боковой p-n-p 0,005-10 0,25 [8]
Вертикальный p-n-p 0,02-40 0,30 [8]
LM111 0,02-20 0,32 [9]
2N2907 10-2000 0,16 [10]
n-p-n (BC817) 0,04-100 0,22 [11]
p-n-p (BC 807) 0,2-200 0,14 [11]
Полученные результаты приведены в табл. 3.
Из данных таблицы следует, что используемые в расчетной методике диапазон интенсивностей 0,05-100 Р/с и значения коэффициента m=0,26 не могут быть применены для оценки стойкости биполярных полупроводниковых приборов. Наиболее близкое значение коэффициента m=0,25 у бокового p-n-p транзистора, но в диапазоне интенсивностей 0,005-10 рад/с.
Во втором случае при определении дифференциального показателя степени m для каждого значения интенсивности находилось значение производной функции, показанной на рис. 6. Тем самым измерялось дифференциальное значение наклона в каждой точке кривой. В этом варианте использование степенной аппроксимации вида (1) справедливо в окрестности заданного значения мощности дозы.
Результаты расчетов приведены на рис. 8. При очень малых и очень больших значениях интенсивности показатель m=0, что соответствует насыщению величины дозы отказов при малых и больших мощностях доз. В интервале интенсивностей, где зависимость допустимой мощности дозы от интенсивности нелинейна, показатель степени m меняется для разных приборов в широком интервале. Как правило, показатель степени принимает максимальное значение приблизительно в середине интервала, соответствующего границам диапазона интенсивностей, в котором определялось интегральное значение коэффициента m. Величина максимального значения коэффициента m для разных приборов изменяется в диапазоне 0,24-0,55. Использование рекомендованного в [6] значения m=0,26 для всех биполярных приборов может приводить к существенным ошибкам в прогнозировании предельной дозы отказов. Указанный в [6] диапазон интенсивностей 0,05-100 рад(SiO2)/с, где рекомендовано применение показательной функции (1), справедлив только для транзистора n-p-n (BC817).
Заключение
Использование степенной функции для моделирования эффекта низкой интенсивности в биполярных приборах, как показал анализ экспериментальных данных, требует осторожности. Выбор универсального значения показателя степени m=0,26 для всех типов биполярных приборов нельзя считать обоснованным. Стандарты США (MIL-STD 883H) и Европейского космического агентства (ESA/SCC), дающие консервативную оценку на наихудший случай, без учета конкретных условий эксплуатации приборов на орбите, также требуют существенного усовершенствования для повышения достоверности прогнозирования работоспособности микросхем, содержащих биполярные приборы в условиях воздействия факторов космического пространства. Поэтому необходимо продолжить работы по созданию физической модели и методик прогнозирования эффекта низкой интенсивности в приборах, содержащих биполярные транзисторы.
Литература
Enlow E.W., Pease R.L., Combos W.E. et al. Response of advanced bipolar processes to ionizing radiation. // IEEE Trans. Nucl. Sci. 1991. Vol. 38, N. 6. P. 1342-1351.
MIL-STD 883H (Method 1019,4).
Стандарт Европейского космического агентства ESA/SCC.
Руководящий документ РД В 319.03.37-200.
Отраслевой стандарт Российского космического агентства ОСТ 134.
Малышев М.М., Малинин В.Г., Ванин В.И. Оценка ресурса изделия электронной техники в условиях низкоинтенсивного облучения // Вопросы атомной науки и техники. Сер. Физика радиационного воздействия на радиоэлектронную аппаратуру. 1998. Вып. 1-2. С 25-130.
Першенков В.С., Савченков Д.В., Бакеренков А.С., Улимов В.Н. Консервативная модель эффекта низкой интенсивности в биполярных микроэлектронных структурах при воздействии ионизирующего излучения // Микроэлектроника, 2010. Т.39, № 2. С. 102-112. |
| Категория: Конспекты (курсы КП и ПК) | Добавил: Earlinger (06.09.2013)
| Автор: Елизаров Кирилл
|
| Просмотров: 906
| Рейтинг: 0.0/0 |
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
|