Научно-исследовательский ядерный университет
Московский инженерно-физический институт
Факультет «Автоматики и электроники»
Кафедра «Микро- и наноэлектроники»
Моделирование преследования
Человек и лев
Преподаватель: доцент В.А. Лапшинский
Подготовил студент группы А4-11: Полянский А.Д.
Легенда
Пусть имеется два точечных тела. Одно в центре круга, а другое на круге радиусом R. Пусть эти тела одновременно начинаю движение со скоростями V1 и V2. Причем первое тело всегда двигается в направлении второго, поскольку «хочет» его догнать. При каких условиях это может случиться?
Моделирование
Для решения этой задачи, нужно сделать несколько упрощений для того, чтобы разобраться с некоторыми неопределенностями. Во-первых, если скорость человека может менять направление сколько угодно быстро, то возникают бесконечно большие ускорения (ведь скорость векторная величина), поясню: предположим, человек бежал в одну сторону со скоростью V и увидел, что лев его в следующую секунду настигнет, тогда он за бесконечно малый промежуток времени меняет свое направление движения на 180 градусов и бежит уже в обратном направлении, поскольку скорость векторная величина, то изменение скорости равно уже 2V.По определению ускорение – это производная скорости по времени. Следовательно, ускорение равно 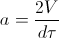 (dv=2V), причем dt стремиться к 0 и da стремиться к бесконечности, в этом случае лев его настигнет только тогда, когда его скорость будет большей, чем скорость человека. И, честно говоря, всегда, когда скорость льва больше скорости человека, то через какое-то время T, лев догонит человека (при условии, что человек движется по окружности).Если человек движется внутри круга (по арене) в любую сторону, то при условии возможности человека менять скорость мгновенно, лев никогда не настигнет человека. Доказательство можно найти в интернете.
Поэтому определим движение человека только по окружности с постоянной скоростью и постоянным направлением движения. Тогда уравнения его движения задаются формулами (1) и (2):
 (1)
 (2)
Так как через любые две точки можно провести прямую и притом только одну, то всегда можно направить ось x так, чтобы она проходила через начальное местоположения человека на круге и льва (который находится в центре круга, то есть начало координат в центре круга).
Из условия задачи лев движется всегда в направлении человека, попытаемся найти уравнение движения для льва. Угловая скорость движения человека равна 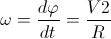 .Этот путь будет соответствовать углу dφ=ωdt. Уравнение льва задается прямой y=kx, где k есть tg(dφ).Далее с помощью простых математических преобразований при бесконечно малых величинах получим, что tg(dφ)=V2/Rdt.Получим уравнение прямой, вдоль которой движется лев (3):
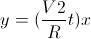 (3)
Вдоль этой прямой лев движется со скоростью V1 и пройдет путь равный S=V1t. Чтобы получить уравнение движения надо воспользоваться теоремой Пифагора, то есть, зная по которой прямой движется лев, мы знаем, что должно выполняться соотношение (4):
y2+x2=(V1t)2 (4)
Из этих двух уравнений получим уравнения движения льва.Чтобы получить время встречи, надо приравнять x и y соответственно в уравнениях движения льва и человека.Возведя уравнения в квадрат и сложив их, получим уравнение для времени (5), которое равно:
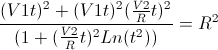 (5)
Решив данное уравнение и сделав замену t2=p.Получим уравнение(6) для p:
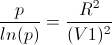 (6)
Решая это уравнение,найдем p.И время будет равно арифметическому квадратному корню из p.
Анализируя полученное уравнения для времени, мы можем заметить, что оно не зависит от скорости убегающего человека, это связанно с тем, что он всегда движется по окружности, не меняя направления своего движения, это приводит к тому, что встреча все равно произойдет, то есть как только лев достигает окружности, он начинает двигаться навстречу человеку, а человеку соответственно сам бежит ко льву в пасть.
Результаты моделирования
Из диаграммы видно, что шансы догнать человека у льва есть всегда, если человек будет просто бегать по кругу, если лев будет бежать в направлении человека всегда, то это займет чуточку больше времени, чем, если бы лев бежал сразу в ту точку окружности, где будет человек через время, нужное льву достигнуть этой точки.
Список Литературы
1. http://www.valinfo.ru/ - сайт для тех, кто хочет знать.
2. http://www.google.ru/ - сайт для тех, кто знает, что искать.
|
