Национальный исследовательский ядерный университет «МИФИ» Факультет: «Автоматика и электроника» Кафедра: «Микро- и наноэлектроника»
Предмет: «Компьютерный практикум˗13»
Предел Бреммерманна против закона Мура Группа: А4-09 Выполнил: Хайбуллин Ч.И. Преподаватель: доц. Лапшинский В.А. Москва 2013
Содержание
Аннотация……………………………………………………...3
Глоссарий………………………………………………………3
Легенда....................................................................................... 4
Результаты.................................................................................. 5
Заключение……………………………………………………..7
Источники................................................................................... 7
Аннотация
В данной статье рассматривается
предел Бремерманна и закон Мура. Предпринята попытка расчета времени до
достижения предела Бреммермана против закона Мура.
Глоссарий
Транзистор — радиоэлектронный компонент из полупроводникового материала, обычно с тремя
выводами, позволяющий входным сигналом управлять током в электрической цепи.
Процессор —
электронный блок либо интегральная схема (микропроцессор), исполняющая машинные
инструкции (код программ), главная часть аппаратного обеспечения компьютера или
программируемого логического контроллера.
Легенда
Зако́н Му́ра — эмпирическое наблюдение, изначально
сделанное Гордоном Муром, согласно которому (в современной формулировке)
количество транзисторов, размещаемых на кристалле интегральной схемы, удваивается
каждые 24 месяца. Часто цитируемый интервал в 18 месяцев связан с прогнозом
Давида Хауса из Intel, по мнению которого производительность процессоров должна
удваиваться каждые 18 месяцев из- за
сочетания роста количества транзисторов и быстродействия каждого из них.
Закон Мура, не единственный закон дающий
количественную характеристику росту вычислительных мощностей, но нас он
интересует сейчас в силу своей простоты и линейной зависимости, от мощности
компьютеров.
Существует также предел Бреммерманна. Он гласит что
максимальная возможная вычислительная единица равна 1,36×10^50 Бит/(секунду × грамм).
Собственно, наша задача посмотреть как далеко мы от
этого идеального источника. Для этого у нас есть вся информация. Результаты По ходу сбора информации и анализа данных, стало
понятно что полноценный анализ не представляется возможным, потому что мощность
компьютера в целом характеризуется не только частотой процессора (количеством
операций в секунду), но также многими другими параметрами. Поэтому была создана
модель, которую характеризуют две величины , число транзисторов и тактовая
частота процессора. Результатом анализа этих данных стал график. 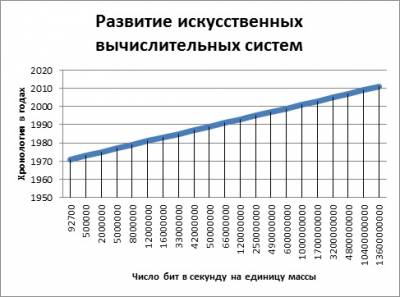
Согласно этому графику был высчитан коэффициент
увеличения вычислительной мощности на единицу времени на единицу массы. Его
среднее значение до 2007 года составляет
1,52 , а после до 2011 года 1,36 – это различие объясняется переходом от
одноядерных домашних систем к многоядерным. Используя этот коэффициент не
трудно посчитать количество лет требуемых человечеству для достижения предела
Бреммерманна против закона Мура. 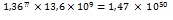
Откуда найдем x , а значит, количество, раз на которое нужно умножить число бит\с в 2011 году,
чтобы прийти к пределу Бремерманна. 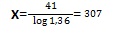
Таким образом ответ 307 лет при нынешних темпах
развития необходимо чтобы достичь предела Бреммерманна. Заключение . Ответ
получился поразительным 307 лет. Несмотря на то что число транзисторов растет геометрически,
мощности сохраняют линейную зависимость и как следствие закон Бреммерманна
становится очень далекой целью. Кроме того, подсчитано, что к 2020 закон Мура
прекратит свое действие окончательно (он и сейчас допускает неточности,
поскольку транзисторы удваиваются каждые полтора года) поскольку размер
транзистора станет равным , размеру человеческой клетки, но это противоречит
квантовой физике. Источники информации http://www.electrosad.ru/Processor/ProcTech3.htm - статья о развитие процессоров.
Автор А.Сорокин июль 2009 г. http://en.wikipedia.org/wiki/List_of_Intel_microprocessors
- список микропроцессоров intel
для составляния таблицы Excel. http://valinfo.ru/ - некоторые темы форумов, для
работы в Excel , а также общая информация по закону мура и пределу
Бреммерманна.
|