Олимпиада "Наноэлектроника"
Неофициальный сайт

НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ЯДЕРНЫЙ УНИВЕРСИТЕТ

 

Московский инженерно-физический институт

         

Факультет «Автоматики и электроники»

Кафедра «Микро- и наноэлектроники»

«Компьютерный практикум-15»

 

 

 

 

 

 

 

 

 

Домашнее задание №2. МОДЕЛЬ и МОДЕЛИРОВАНИЕ (MS.EXCEL). Закон Мура для CPU

Студент группы А04-09:

 Гусейнова Н.А.

Лысенко А.С.

Преподаватель:

доцент Лапшинский В.А.

 

 

 

Москва 2015

(версия 3.0, Четверг, 28 мая 2015 г.)

Оглавление

Аннотация................................................................................................ 3

 

Введение ................................................................................................3

 

Закон Мура для CPU................................................................................................ 4

            Легенда................................................................................................ 4

            Прогнозирование................................................................................................ 7

 

Тестирование................................................................................................ 10

 

Заключение................................................................................................ 11

 

Список литературы................................................................................................ 11

Приложение................................................................................................ 12

 

 

 

 

ФИО	Excel-1	Excel-2.	Excel-3.	Excel-5.	История	Рейтинг	АТ-2
Гусейнова	87.90%	88.90%	96.30%	90.00%	78.50%	0,89	7,5
Лысенко	98.00%	84.90%	89.20%	93.60%	90.00%	0,90	4,5

Таблица успеваемости студентов

 

             

 

 

 

Аннотация

Главная цель данного домашнего задания- познакомиться с законом Мура для CPU, на примере количества транзисторов в процессорах фирмы Intel построить прогноз на ближайшее будущее, а также подтвердить или опровергнуть действие закона Мура на количество транзисторов.

 

Введение

В 1965 году один из основателей Intel Гордон Мур в процессе подготовки выступления обнаружил закономерность: появление новых моделей микросхем наблюдалось спустя примерно год после предшественников, при этом количество транзисторов в них возрастало каждый раз приблизительно вдвое. Мур пришел к выводу, что при сохранении этой тенденции мощность вычислительных устройств за относительно короткий промежуток времени может вырасти экспоненциально. Это наблюдение получило название — Закон Мура.

В 1975 году Гордон Мур внёс в свой закон коррективы, согласно которым удвоение числа транзисторов будет происходить каждые два года.

Проверим, актуален ли закон Мура на сегодняшний день. Для этого сначала разберем существующие на данный момент времени данные, а после составим прогноз до 2030 года.

 

 

Закон Мура для CPU

Легенда

 

 

N0 — количество транзисторов на кристалле в некоторый год (условно считаем его нулевым),
N(y) — число транзисторов на кристалле спустя лет,
yy — срок (в годах и долях года) за который число транзисторов возрастает вдвое.

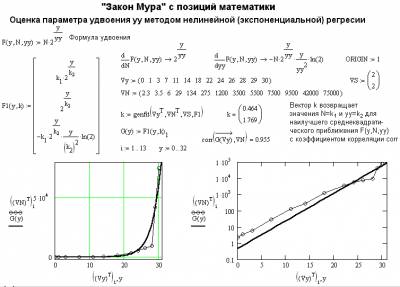
Рис.1 Математическое описание закона Мура

На рисунке 1 представлен закон Мура с точки зрения математики, так что, имея исходные данные, можно рассчитать приблизительную зависимость количества транзисторов а процессоре.

В левом верхнем углу документа задана формула «закона Мура» и в аналитическом виде вычислены ее частные производные по искомым параметрам N и yy. Затем заданы векторыF1 (функции и ее производных, нужных для реализации алгоритма нелинейной регрессии), числа лет прошедших с 1971 года Vy и числа тысяч транзисторов на кристалле процессора VN.

Левый график задает число транзисторов как функцию от параметраyy(время удвоения) в линейном масштабе. При этом расчетный график имеет типично экспоненциальный вид. Он показывает особенно резкое нарастание числа транзисторов в микропроцессорах, начиная с 90-хгодов прошлого века.

Интереснее выглядит расчетный график в логарифмическом масштабе (справа внизу). Он превращается в прямую, наклон которой определяется параметром yy. В течении первых примерно двадцати лет расчетный график приближающей функции и график, построенный по точкам реальных данных, идут практически параллельно, что свидетельствует о справедливости оценок Мура на протяжении этого времени. При этом реальное число транзисторов в серийных микропроцессорах оказывалось несколько большим, чем при расчетной оценке. Найденное время yy при этом составило 1.769 года, т.е. удвоение числа транзисторов происходило примерно за два года. Ранние оценки времени в полтора года и даже в один год нелинейной регрессией не подтверждаются (Intel отказалась от них) [1].

На таблице 1 представлены сведения о микропроцессорах фирмы Intel до 2001 года, подтверждение закона МУРа графически представлен на рис.2

 Таблица 1. Зависимость типа микропроцессора Intel от количества транзисторов до 2001 года 

Тип микропроцессора	Количество транзисторов, тыс.	Год разработки	Параметр y
4004	N0=2,3	1971	0
8008	3,5	1972	1
8080	6	1974	3
8088	29	1979	8
286	134	1982	11
386	257	1986	15
486	1200	1989	18
Pentium	3500	1993	22
Pentium PRO	550	1995	24
Pentium II	7500	1997	26
Pentium III	9500	1999	28
Pentium 4	42000	2000	29
Pentium 4 M	75000	2001	30

 

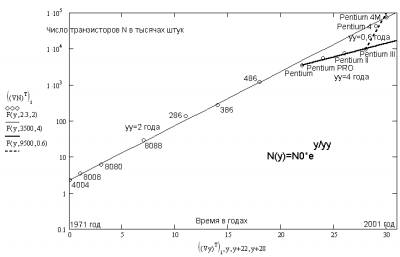
Рис.2. Графическое изображение закона Мура для CPU

 

 

Прогнозирование

            Дополним таблицу, использованную в прошлом пункте, современными данными (Таблица 2) и представим прогноз на ближайшие несколько лет [2].

Таблица 2. Зависимость количества транзисторов от года разработки до 2012

 

Тип микропроцессора	Количество транзисторов,N, тыс.	Год разработки	Log10(N)
4004	N0=2,3	1971	0,36
8008	3,5	1972	0,54
8080	6	1974	0,78
8088	29	1979	1,46
286	134	1982	2,13
386	257	1986	2,41
486	1200	1989	3,08
Pentium	3500	1993	3,54
Pentium PRO	5500	1995	3,74
Pentium II	7500	1997	3,88
Pentium III	9500	1999	3,98
Pentium 4	42000	2000	4,62
Pentium 4 M	75000	2001	4,88
Intel Core I3(N)	382000	2008	5,58
Intel Core I3(SB)	624000	2009	5,8
Intel Core I5	774000	2010	5,89
Intel Core I7(N)	1170000	2011	6,07
Intel  Core I7(SB)	2270000	2012	6,36

 

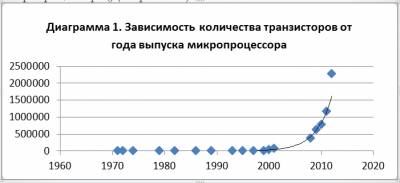
С помощью функционала Microsoft Office  можно построить график зависимости количества транзисторов от года выпуска микропроцессора (Диаграмма 1).

 Чтобы построить прогноз, использован полулогарифмичесий график зависимости количества транзисторов от года выпуска микропроцессора (Диаграмма 2).

 

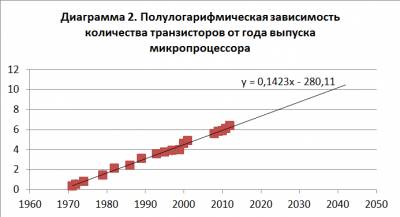
     Вывод: как видно по данным таблицы и предоставленным графикам, закон Мура для транзисторов микропроцессоров фирмы Intel выполняется, то есть приблизительно каждые два года происходит удвоение количества транзисторов.

 

Тестовый контент

Вариант 4. MS.Excel. Функционал. Условное форматирование [5]

 

Вопрос 1:Что позволяет делать условное форматирование:

1. *Применять форматирование ячеек избирательно или автоматически на основании их значений
2. Проводить ёфикацию и проверку орфографии
3. Менять ориентацию
4. Менять цвет страницы
5. Создавать примечания

 

Вопрос 2: Выберите виды условного форматирования

1. *[0.33] Гистограммы
2. *[0.33] Наборы значков
3. Диаграммы
4. *[0.33] Цветовые шкалы
5. Выравнивание

 

Вопрос 3:  Можно ли с помощью условного форматирования определить ячейки с ошибочными записями или значениями определенного типа?

Ответ: Да [3].

 

Вопрос 4: Что такое условное форматирование?

Ответ: Условное форматирование - применение стиля ячейки в зависимости от условия [4].

 

 

 

Заключение

                   В данном домашнем задании была проведена работа с Microsoft Exsel, рассмотрена работа с моделирование, корреляцией и регрессией.

                   По конкретной теме домашнего задания было установлено: для микропроцессоров фирмы Intel выполняется закон Мура, то есть число транзисторов увеличивается вдвое приблизительно каждые два года.

 

Список литературы

1. http://www.cnews.ru/reviews/?2003/07/14/146261 -  Тайны «Закона Мура»
2. https://ru.wikipedia.org/wiki/%D0%A1%D0%BF%D0%B8%D1%81%D0%BE%D0%BA_%D0%BC%D0%B8%D0%BA%D1%80%D0%BE%D0%BF%D1%80%D0%BE%D1%86%D0%B5%D1%81%D1%81%D0%BE%D1%80%D0%BE%D0%B2_Intel - Микропроцессоры Intel
3. http://exceltip.ru/%D1%83%D1%81%D0%BB%D0%BE%D0%B2%D0%BD%D0%BE%D0%B5-%D1%84%D0%BE%D1%80%D0%BC%D0%B0%D1%82%D0%B8%D1%80%D0%BE%D0%B2%D0%B0%D0%BD%D0%B8%D0%B5-%D0%B2-excel/ - Условное форматирование в Excel
4. https://wiki.openoffice.org/wiki/RU/kb/00000103 - База знаний. Условное форматирование.
5. http://www.valinfo.ru/forum/index.php?showtopic=4368&hl=%EA%EF-15 - КП-15. АТ-2 (к ДЗ №2) Excel (вопросы и ответы), моделирование прогнозов.

Приложение

                   На рис.3 представлен файл таблицы  excel, которая лежала в основе диаграмм для составления прогноза.

 

                 

 Рис. 3. Таблица Excel для создания прогноза

Коэффициент корреляции (r) равен 0.997

Связь между исследуемыми признаками - прямая, теснота (сила) связи по шкале Чеддока - функциональная

Число степеней свободы (f) составляет 16

t-критерий Стьюдента равен 54.861

Критическое значение t-критерия Стьюдента при данном числе степеней свободы составляет 2.12. tнабл > tкрит, зависимость признаков статистически значима (p<0,05)

 

Уравнение парной линейной регрессии: y = -280.28905 + 0.14240 * x

Коэффициент детерминации r2 равен 0.995 (факторный признак x определяет 99.5% дисперсии зависимого признака y)

Средняя ошибка аппроксимации (характеризует адекватность регрессионной модели) составляет 3.4%[1]

[1] Источник:  http://medstatistic.ru/calculators/calccorrelation.html?nums=18 - калькулятор для расчета корреляции и регрессии.